Lección del juego: "Formulas de Multiplicación Reducida"

Objetivos:
Educación:

• Resumir y sistematizar el conocimiento de los estudiantes sobre este tema.
• Desarrollar las habilidades de usar fórmulas de multiplicación reducidas al resolver tareas.
• Prepárense para el control.

Desarrollo:

1. Desarrollar interés cognitivo y ampliar los horizontes de los estudiantes.
2. Aprende a aplicar el conocimiento en la práctica.

Educación:

1. Educar habilidades y habilidades de los estudiantes en el equipo.

Tipo de lección: una lección de repetición generalizada.

Equipo: instalación multimedia.

Progreso de clase

Diapositiva 1-2.

1. Momento de organización

Diapositiva 3.

El álgebra no es más que un lenguaje matemático adaptado para denotar las relaciones entre las cantidades.
Y Newton

Diapositiva 4.

2. Las reglas del juego "Mathematical sea battle".

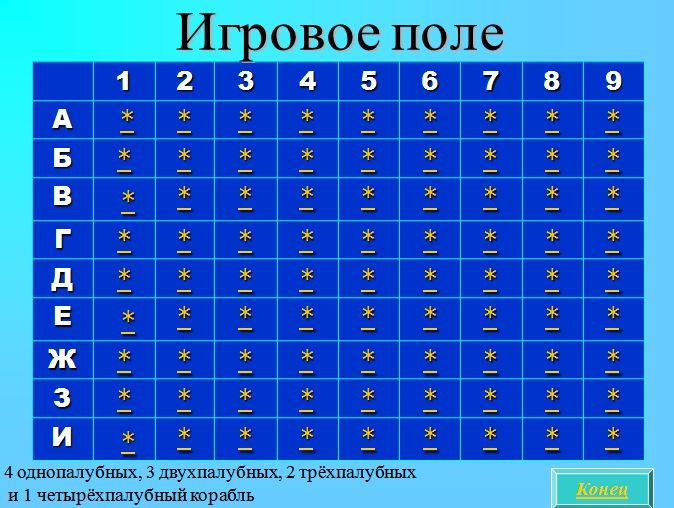
• Para el juego, la clase se divide en 2 grupos. Los equipos disparan alternativamente a los barcos, nombrando las celdas del campo de juego (slide 5). Al presionar el símbolo * en la celda especificada, se verifica la efectividad del movimiento.
• Si uno de los equipos cometió un error, el movimiento pasa (slide 6), si una referencia histórica cae, después de familiarizarse con él, el equipo tiene derecho a otro movimiento, si todos los equipos son alcanzados, se ofrece la tarea. El derecho prioritario de respuesta se da al equipo que hizo un movimiento exitoso. Si este equipo comete un error, los oponentes responden. Los puntos se otorgan al equipo que dio la respuesta correcta.
• El tiempo para completar la tarea es limitado. Después del tiempo asignado, revisamos la respuesta. Al hacer clic en la palabra "puntos" vamos a la tabla de resultados (slide 25) e ingresamos los puntos al equipo que correctamente completó la tarea. Luego, haciendo clic en la palabra "back" de nuevo volver al campo de juego (slide 5).

Diapositiva 5.

3. Asignaciones para la aplicación

Preguntas para el trabajo oral.
Diapositiva 7.
A-1. ¿Cuál es la diferencia entre las dos expresiones? (2 puntos)
Diapositiva 8.
A-5. ¿Cuál es el cuadrado de la suma y el cuadrado de la diferencia de dos expresiones? (2 puntos)
Diapositiva 9.
A-6. ¿Cuál es la suma de cubos y la diferencia de cubos de dos expresiones? (2 puntos)
Diapositiva 10.
A-7. ¿Cuál es el cuadrado de la suma de tres expresiones? (2 puntos)
Diapositiva 11.
A-9. ¿Cuál es el cubo de la diferencia y el cubo de la suma de dos expresiones? (2 puntos)

Tareas para realizar en el cuaderno.

Diapositiva 12.
B-1. Imagina la expresión polinomio(2m+5)(5-2m+4m)²(4 puntos).
Respuesta: 25
Diapositiva 13.
B-3. Imagina la expresión polinomio (2x+3)²- 4x2 (4 puntos).
Respuesta: 12x+9
Diapositiva 14.

B-4. Imagina la expresión polinomio(2x-3u)²+(3x+2u)²(4 puntos).
Respuesta: 13x²+13²
Diapositiva 15.

B-5. Imagina la expresión polinomio (2x-3)(2x+3)-(2x-1)²(4 puntos).
Respuesta: 4x-10
Diapositiva 16.

B-6. Imagina la expresión polinomio (2x+y)³-6hu(2x+y) (4 puntos).
Respuesta: 8x³+³
Diapositiva 17.

B-9. Piense en la expresión polinomio (m-n)³+3mn(m-n) (4 puntos).
Respuesta: m³ +n³
Diapositiva 18.

D-8. Multiplique los polinomios (2x+1)²-16 (6 puntos).
Respuesta: (2x-3)(2x+5).

Slide 19.
E-2. Multiplique el polinomio (x -2)²-(x+1)²(6 puntos).
Respuesta: -3(2x-1)

Diapositiva 20.
G-4. Imagínate en forma de trabajo x6 -27 (8 puntos).
Respuesta: x)²-3)⁴+3x²+9)

Diapositiva 21.
G-5. Convertir en polinomio (3x+y2)³(8 puntos).
Respuesta: 27x³+27x²у²+9ha⁴+u6

Diapositiva 22.
G-7. Resolver la ecuación: 4x2+4x+1=0 (10 puntos).
Decisión
4x²+4x+1=0
(2x+1)²= 0;
2x+1=0;
2x=-1;
x=1:2;
x = 0,5.
4·0,5² + 4·0,5+1=0.
0=0
Respuesta: 0.5
Diapositiva 23.
G-8. Resolver la ecuación: (7x)²-(x-8)(x+8) = 43 (10 puntos).
Solución.
(7x)²-(x-8)(x+8) =43;
72-2·7·х+х²- x2-82) = 43;
49-14x+x²-²+44=43;
-14x=-70;
x=-70:14;
x=5.
(7 a 5)²-(5-8)(5+8)=43
43=43.
Respuesta:5
Diapositiva 24.
E-2. Encuentra el valor más bajo del trimember cuadrado x2 +2 x +7 (12 puntos).
Solución.
x2 +2 x +7=(x)² +2·1·х+12)-12+7=(х+1)²+6
Este tres plazo supone el valor más bajo cuando (x+1)2 toma el valor más bajo, es decir (x+1)²= 0.
Por lo tanto, el valor más pequeño de un cuadrado tres términos es 6.
Respuesta: 6
Diapositiva 25.
E-3. A qué valor x de cualquier valor x cuadrado tres términos x²-12x+50 es el menos importante? (12 puntos).
Solución.
х²-12x+50=x²-2·6·х+36)-36+50 = (х-6)²+14
Esta triada es la menos importante cuando
(x-6)²= 0;
x-6=0;
x=6.
Respuesta: 6
Diapositiva 26.
E-4. Premio (6 puntos).

4. Antecedentes históricos
Dado que las fórmulas de la multiplicación abreviada se estudian en la clase de álgebra, estas referencias históricas te permitirán aprender de dónde vino este nombre y de qué científicos han hecho una gran contribución al desarrollo de esta ciencia.
Diapositiva 27.

• La palabra "Álgebra" surgió después de la aparición del tratado del matemático y astrónomo Mohammed ben Musa al-Khwarizmi (787-oc.850). El término al-Jabr, tomado del título de este libro, fue utilizado posteriormente como álgebra.

Slide 28.

• Muhammad Al-Khwarizmi (787–unos 850) escribió los tratados fundamentales sobre aritmética y álgebra.

Diapositiva 29.

• Diophantus Alexandrovsky (siglo III). En su libro “Arithmetic” hay rudimentos de simbolismo de letras y notaciones especiales para grados, así como un signo igual, un breve registro de las reglas de la multiplicación, problemas que conducen a sistemas complejos de ecuaciones algebraicas.

Diapositiva 30.

• François Viet (1540-1603) introdujo símbolos algebraicos, comenzó a denotar números con letras, desarrolló los fundamentos del álgebra.

Diapositiva 31.

• Pierre Fermat (1601-1665) estaba comprometido en la teoría de resolver ecuaciones algebraicas con varias variables.

Diapositiva 32.

• René Descartes (1596-1650) amplió el número de números con los que se podían realizar acciones. Presentado :x, y, z - variables, desconocidos; a, b, c - constantes, parámetros; signo de división.

Slide 33.

• Gottfried Wilhelm Leibniz (1446-1716) creó las bases del análisis matemático, introdujo muchos conceptos y símbolos.

Slide 34.
5. Resultados de la experiencia. Contando puntos y premiando al equipo ganador.

35.
Revisando la ubicación de los barcos.

6. Homework.

{module Google_kvadrat}

Presentación en formato .ppt y resumen de la lección en formato .doc de 2.54 Mb